Segel Wissen

Segelmacher informiert über die Grundlagen der Strömungsmechanik

Um die Wirkungsweise der Segel eines Segelschiffes besser zu verstehen, betrachten wir einige wichtige Grundlagen der Strömungsmechanik. Vereinfacht gesehen besteht ein Segelboot aus vier Elementen: Segel, Rumpf, Kiel und Ruder. Jedes Element für sich ist ein Tragflügel.

Das Zusammenspiel der Kräfte, die durch die Tragflügelwirkung entstehen, beschreibt das Segelverhalten. Kiel und Ruder befinden sich im Wasser, das Segel in der Luft, der Rumpf in beiden Medien. Unterschiede und Gemeinsamkeiten von Segel – Luft und Wasser bilden die Grundlage.

Damit man sich nicht in Details verliert, die auf die Gesamtwirkung einen zu vernachlässigenden Einfluss besitzen, werden Annahmen getroffen, die zu einer übersichtlichen Theorie führen. Die Theorie der Segel – Ideale Flüssigkeiten  geht beispielsweise davon aus, dass die Luft inkompressibel ist. Der Fehler, der dadurch entsteht, beträgt bis zu einer Geschwindigkeit von 100 Knoten weniger als 1 Prozent – ein akzeptabler Wert.

Die beiden entscheidenden Kräfte am Segel, Auftrieb und Widerstand. Wir betrachten zunächst die Theorie der Potentialströmung am Segel, um hieraus die wesentlichen Grundlagen für das weitere Verständnis zu entwickeln.

Eine der entscheidenden Gleichungen für das Verständnis von Aero- und Hydrodynamik am Segel – ist die Bernoulli Gleichung. Sie setzt Geschwindigkeit und Druck einer Flüssigkeit miteinander in Beziehung.

Die Grenzschichttheorie nach Prandtl löst ein scheinbares Paradoxon in der Theorie der reibungslosen Flüssigkeiten. Segel und Grenzschichttheorie. Mit Hilfe der Rotationsströmung wird unter anderem verständlich, warum ein Tornado weiß ist. Rotationsströmungen am Segel.

Wir leiten die Auftriebskraft ab aus der Überlagerung einer Parallelströmung mit einer Zirkulationsströmung um einen Kreiszylinder. Zusammen mit der Bernoulli Gleichung ergibt sich die Segel – Auftriebskraft als Druckdifferenz zwischen Oberseite und Unterseite des Kreiszylinders.

Segelmacher informiert über Segel und Tragflügel in Luft und Wasser

 

Idealisiert besteht ein Segelboot aus einem Segel, Rumpf, Kiel und Ruder. Die wesentlichen Kräfte dieser vier Elemente werden durch die Tragflügelwirkung erzeugt. Das Segel ist dabei auf den ersten Blick auch als Tragflügel zu erkennen. Gerade die neuen Segelmaterialien lassen ein modernes Segel exakt wie ein Tragflügel erscheinen. Doch auch der Rumpf mit dem Kiel verhält sich wie ein Tragflügel, dessen Querkraft der vom Segel erzeugten Seitenkraft entgegen wirkt. Und auch das Ruder ist nichts anderes als ein beweglicher Tragflügel. Mittels der Auftriebskräfte des Ruders wird das Schiff gesteuert. An einem Tragflügel wirken im Wesentlichen zwei Kräfte: Der Widerstand und der Auftrieb. Der Auftrieb wird auch als Querkraft bezeichnet. Je nach Anstellwinkel des Tragflügels ist die Auftriebskraft wesentlich stärker als der Widerstand. Dies ist im Wesentlichen die Ursache dafür, dass ein Flugzeug fliegt und ein Segelboot am Wind segeln kann.
Die Wirkungsweise eines Segels ist also vergleichbar mit der eines Tragflügels. Daher werden Erkenntnisse aus der Theorie der Flugzeugtragflügel auf Segel, Kiel und Ruder angewandt. Dies ist ohne große Fehler möglich, da bei relativ kleinen Geschwindigkeiten sich Wasser wie Luft verhält. Zwei Dinge müssen nur berücksichtigt werden: Zum einen sind es andere Zahlenwerte für Dichte, Zähigkeit und ähnliche Größen, und zum anderen kommt beim Rumpf noch der Faktor des Wellenwiderstandes dazu. Bei den tief eingetauchten Anhängen des Rumpfes sowie beim Kiel und Ruder verhält sich jedoch das Wasser genauso wie die Luft. Daher werden wir Luft und Wasser als Bestandteile derselben Gattung, nämlich Flüssigkeiten, auffassen.

zurück nach oben

Segel in idealer Flüssigkeit und zweidimensionale Strömungen

 

Segel, Rumpf, Kiel und Ruder sind von Flüssigkeit umgeben. Um die Auftriebskräfte am Segel zu beschreiben ist es sinnvoll, ein paar Annahmen über die umgebende Flüssigkeit zu machen. In der Beschreibung der Segel werden in der Strömungstheorie daher folgende vereinfachende Annahmen getroffen. Bei der Flüssigkeit geht man davon aus, dass sie das Segel, bzw. den Tragflügel, reibungslos umströmt. Das bedeutet in der Theorie, dass keine Energieumwandlung von kinetischer Energie in Wärmeenergie, infolge der Reibung, berücksichtigt werden muss.

Desweiteren trifft man die Vereinfachung, dass die Beschaffenheit der Flüssigkeit homogen ist, dass sie also an allen Stellen dieselbe Eigenschaft in Form von Zähigkeit, Dichte etc. hat. Eine weitere Annahme ist, dass die Flüssigkeit inkompressibel ist. Das bedeutet, dass man sie nicht einfach zusammendrücken kann, sondern dass dies nur im Einklang mit einer Druckerhöhung erfolgt.

Die nächste Annahme betrifft das Strömungsmodell. Hier stellt man sich den Tragflügel unendlich lang vor, so dass man es im Prinzip nur mit einer zweidimensionalen Strömung zu tun hat, da die dritte Dimension keine Änderung mehr mit bringt. Man vernachlässigt auf diese Art und Weise das Tragflügelende, um das herum sich in der Realität komplizierte Strömungen bilden. Diese Turbulenzen sind jedoch weder nützlich noch hilfreich bei der Beschreibung der Auftriebskräfte eines Tragflügels bzw. des Segels. In Windkanalversuchen passt man hierzu den Tragflügel zwischen zwei vertikalen Endseiten ein, so dass das Ende des Tragflügels quasi abgeschnitten wird.

zurück nach oben

Segel und Potentialströmung

 

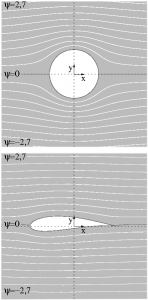
Potentialströmung um Zylinder & Flügelprofil

Die auftretenden Kräfte an einem Segel oder an einem Körper in einer Flüssigkeit haben ihren Ursprung zum einen Teil in der Funktion als Hindernis, nämlich dass das Segel bzw. der Körper die freie Strömung der Flüssigkeit stört, und zum anderen Teil in den Strömungsverhältnissen an der Oberfläche des Segels. Beim Segel haben wir beide Kräfte schon kennen gelernt, der Auftrieb am Segel und der Widerstand durch das Segel.

Die Strömungsverhältnisse an der Oberfläche des Segels werden durch Zähigkeitseffekte hervorgerufen. Dieser Reibungswiderstand ist es, der für das Zustandekommen des Auftriebs erforderlich ist. Er ist es aber auch, der die an sich einfachen mathematischen Modelle kompliziert macht.

Hilfreich für das Verständnis ist die Betrachtung einfacher Stromlinien um einen Kreiszylinder. Anhand dieses Modells wird die Beziehung zwischen der Form des Segels bzw. des Tragflügels, und den induzierten Geschwindigkeiten, Drücken und Kräften erläutert.

Eine Flüssigkeitsströmung kann man sich als eine Kette von Teilchen vorstellen, die sich alle mit gleicher Geschwindigkeit bewegen. Von einer Potentialströmung sprechen wir, wenn wir stationäre Strömungen meinen. Bei stationären Strömungen ist die örtliche Strömungsgeschwindigkeit konstant. Somit sieht das Stromlinienbild immer gleich aus. Bei instationären Strömungen dagegen ändert die Strömung ständig die Geschwindigkeit, so dass sich die Stromlinien ständig bewegen.

Desweiteren gehen wir bei einer Potentialströmung davon aus, dass keine Ablösung der Strömung vom Tragflügel stattfindet. Die Flüssigkeit schließt sich direkt hinter dem Tragflügel wieder zusammen. In der Realität dagegen haben wir es häufig mit Ablösungen der Strömung zu tun. Um das Prinzip des Auftriebs jedoch zu beschreiben, kann das dieses Phänomen vernachlässigt werden.

zurück nach oben

Segel mit Auftrieb und Bernoulli Gleichung

 

Bernulli Gleichung für Strömung

Wenn man ein Stromlinienbild um ein Segel betrachtet, so symbolisiert der Abstand der Stromlinien voneinander die Größe der Geschwindigkeit um das Segel. Je enger die Stromlinien zusammen rücken, desto größer die Strömungsgeschwindigkeit an dieser Stelle des Segel. Das Stromlinienbild beschreibt also nicht nur die Richtung der Strömung sondern auch die Geschwindigkeit. Es zeigt das Geschwindigkeitsfeld des Segel.

Die Geschwindigkeit einer Strömung um einen Kreiszylinder ist gleich dem Zweifachen der Anfangsgeschwindigkeit der Flüssigkeit multipliziert mit dem Sinus des Winkels, den der jeweils betrachtete Punkt auf dem Zylinder mit dem Fußpunkt des Kreiszylinders bildet.

Die Bernoulli Gleichung stellt nun einen Zusammenhang her zwischen der Geschwindigkeit der Strömung und dem Staudruck der Strömung, sie lautet: Die Summe aus statischem Druck und dynamischem Druck ist gleich dem Gesamtdruck, und dieser ist konstant. Die Gleichung kann aus dem Energieerhaltungssatz abgeleitet werden. Die Gesamtenergie bleibt konstant, und dies ist ja in unserem Fall der Druck, Statischer und Kinetischer.

Hydrodynamica Danielis Bernoulli

Aus der ersten Formel, die die Geschwindigkeit beschreibt, kann man nun mit Hilfe der Bernoulli Gleichung den Druck an jeder Stelle der Flüssigkeit berechnen. Die Gleichung beschreibt den wechselseitigen Austausch zwischen potentieller Energie, in Form des statischen Drucks und der kinetischen Energie in Form des Staudrucks. Nimmt also die Geschwindigkeit der Flüssigkeit zu, und damit die kinetische Energie, so verringert sich im gleichen Maß die potentielle Energie in Form des statischen Drucks.

Man kann den statischen Druck bei zusammengepresster Luft vergleichen mit der potentiellen Energie einer gespannten Feder. Eine weitere Schlussfolgerung aus der Bernoulli Gleichung ist, das mit zunehmender Geschwindigkeit der Druck abnimmt. Gefühlsmäßig erscheint dies nicht logisch, man verbindet hohe Geschwindigkeit eher auch mit hohem Druck. Man muss es aber anders betrachten: dort wo die Geschwindigkeit in einer Strömung abnimmt überträgt sich die Bewegungsenergie in die Form des statischen Drucks, der an dieser Stelle zunimmt. Das was in einer Energieform verloren geht, steht in einer anderen Form wieder auf.

Das bedeutet, dass in einer idealen Flüssigkeit, dort wird keine Energie durch Reibung in Wärme gewandelt, hat die Energieumwandlung nur Geschwindigkeits- und Druckänderungen zur Folge.

In einer realen Strömung, in der durch Reibung ein Teil der kinetischen Energie in Wärme umgewandelt wird, ist der Gesamtdruck nicht mehr konstant. Handelt es sich aber um eine recht langsame Strömung, wie in der Situation eines Segelboots, und um Flüssigkeiten mit sehr niedriger Zähigkeit, wie Wasser und Luft, liefert die Bernoulli Gleichung sehr gute Näherungswerte, da der Anteil der durch Reibung in Wärmeenergie umgewandelten Energie nur sehr gering ist.

zurück nach oben

Segel und Grenzschichttheorie von Prandtl

 

Um die Wirkungsweise des Segels zu verstehen, betrachten wir die Grenzschichttheorie von Prandtl. Sie bringt Theorie und Praxis in Einklang miteinander. Auch beim Segel existiert diese Grenzschicht eng am Segel und sorgt für Verwirbelungen am Segel. In der Theorie der reibungslosen Flüssigkeit ist paradoxerweise die Druckverteilung einer einen rotierenden Zylinder umströmenden Flüssigkeit symmetrisch zur vertikalen und horizontalen Achse. Das bedeutet, dass die Flüssigkeit auf den Zylinder keine Kraft ausübt.
Dieses Paradoxon äußerte sich darin, dass man Dinge beobachten aber nicht beweisen konnte, und dass man Dinge beweisen konnte, die man nicht beobachten konnte. Prandtl löste zu Begin des 20. Jahrhunderts diesen scheinbaren Widerspruch, indem er das Strömungsfeld um einen Körper in zwei Bereiche aufteilte. In dem Bereich, der eng an den Körper heranreicht, wird die Flüssigkeit im wesentlichen durch die Zähigkeit bestimmt. Man bezeichnet sie als Grenzschicht. Im zweiten Bereich, außerhalb der Grenzschicht, wird die Strömung im wesentlichen durch die Theorie der reibungslosen Flüssigkeit beschrieben. In ihr können die Zähigkeitseffekte vernachlässigt werden.
Wir betrachten wieder einen drehenden Zylinder in einer Parrallelströmung. Die Flüssigkeitsteilchen werden an der Zylinderwand abgebremst. Dadurch beginnen sich die Teilchen auf der Rückseite des drehenden Zylinders zu stauen, sie lösen sich vom Zylinder ab. Der Stau wiederum bewirkt ein dicker werden der Grenzschicht. Dadurch werden die Stromlinien gewaltsam von der Zylinderkontur abgedrängt.

Dies bezeichnet man als Ablösung der Strömung, die stromabwärts ein turbulentes Wirbelgebiet zur Folge hat.

zurück nach oben

Segel und Rotationsströmung

 

Um die Theorie des Auftriebs am Segel zu verstehen, betrachten wir als nächstes einen weiteren Strömungsvorgang: die Zirkulationsströmung oder auch Rotationsströmung genannt. Am Segel können wir keine Rotationsströmung direkt, sondern indirekt als Folge der Arbeitsweise des Segels sehen, in Form von Wirbelströmungen. Wirbelströmungen tauchen bei Am-Wind-Kursen hinter dem Segel auf, und durch Zähigkeitseffekte der Luft in der Grenzschicht des Segel.
Unter einer Rotationsströmung verstehen wir eine Strömung, die in konzentrischen Kreisen um einen Zylinder strömt. Man kann eine Rotationsströmung durch drehen eines Zylinders in einer reibungsbehafteten Flüssigkeit erzeugen. Durch die Reibungskraft schleppt der Zylinder die Flüssigkeitselemente mit sich. Die Grenzschicht ist dabei so dünn, dass ihre Auswirkung vernachlässigt werden kann.
Strömungen dieser Art werden auch als Wirbelströmungen bezeichnet, und der Zylinder ist der Wirbelkern. Solche Strömungen kann man in der Natur im Wasser und in der Luft beobachten.

Aus der Bernoulli Gleichung, nach der der Druck dort gering ist, wo die Geschwindigkeit groß ist, kann man folgern, dass der Druck in einer solchen Wirbelströmung im Zentrum besonders gering ist, da die Geschwindigkeit dort am größten ist.

In der Natur, beispielsweise bei Tornados, können wir sehr eindrucksvolle Beispiele beobachten. Im Innern eines Tornados fällt der Druck so stark ab, dass der Wasserdampf in der Luft zu kondensieren beginnt, daher auch sein weißes Aussehen. Hinter Segel-Yachten auf Am-Wind-Kursen entstehen ähnliche Wirbel, die zu Lasten eines ständigen Energieverbrauchs immer neu gebildet werden.

zurück nach oben

Segel und das Prinzip Auftrieb

 

Um die Wirkungsweise eines Segels zu verstehen, bedarf es einiger Grundlagen zum Thema Auftrieb. Die Technik des Überlagerungsprinzips gestattet es eine komplexe Strömung als Überlagerung zweier einfacherer Strömungsvorgänge zu gestalten. Um die komplexen Vorgänge eines Segel zu verstehen, betrachten wir ein einfaches Modell zur Simulation des Segels. Hierzu wollen wir eine reine Parallelströmung mit einer reinen Zirkulationsströmung um einen Kreiszylinder überlagern.

Um das resultierende Strömungsbild, das Geschwindigkeitsfeld, zu erhalten, müssen hierzu die beiden örtlichen Geschwindigkeitsvektoren, die der Parallel- und die der Zirkulationsströmung, addiert werden. Das Problem wird also auf die gleiche Art und Weise gelöst wie die Bestimmung einer resultierenden Kraft als vektorielle Addition der einzelnen Komponenten.

Das Ergebnis zeigt, dass für Punkte auf dem Kreiszylinder die resultierende Tangential-Geschwindigkeit von der reinen Parallelströmung verschieden ist, und zwar in Abhängigkeit von zwei Größen, nämlich der Rotationsgeschwindigkeit des Kreiszylinders, und des Winkels, den der betreffende Punkt auf dem Kreiszylinder mit der Parallelströmung bildet. So ist die Geschwindigkeit auf der Oberseite entsprechend größer, als die der Parallelströmung, und auf der Unterseite entsprechend kleiner.

Aus der Bernoulli Gleichung ergibt sich folglich, dass der Druck auf der Oberseite größer als auf der Unterseite ist. Aus dem Druckunterschied ergibt sich folglich eine resultierende Kraft, die man als Auftrieb bezeichnet. Diese Kraft bewegt den Zylinder nach oben, im rechten Winkel zur Anströmung. Eine Überlagerung von Parallelströmung mit Zirkulationsströmung bewirkt also einen Auftrieb. Eine reine Parallelströmung um einen Zylinder dagegen nicht, die Kräfte halten sich im Gleichgewicht.

Interessant ist ferner die Rollenverteilung zwischen Oberdruck und Unterdruck. Den wesentlichen Beitrag zum Auftrieb übernimmt dabei der Unterdruck auf der Oberseite des Zylinders, der Überdruck auf der Unterseite dagegen ist verhältnismäßig gering.

Ferner kann man zeigen, dass die Größe der resultierenden Kraft, also der Auftrieb, proportional von der Geschwindigkeit der Parallelströmung (genau genommen ist es der aus der Parallelströmung resultierende Staudruck), der Zirkulationsgeschwindigkeit und dem Radius des Zylinders abhängt. Der Proportionalitätsfaktor, auch als Auftriebsbeiwert bezeichnet, ergibt sich als Quotient aus Rotationsgeschwindigkeit und Geschwindigkeit der Parallelströmung.

zurück nach oben